认识神经网络【多层感知器数学原理】
文章目录
- 1、什么是神经网络
- 2、人工神经网络
- 3、多层感知器
- 3.1、输入层
- 3.2、隐藏层
- 3.2.1、隐藏层 1
- 3.2.2、隐藏层 2
- 3.3、输出层
- 3.4、前向传播
- 3.4.1、加权和⭐
- 3.4.2、激活函数
- 3.5、反向传播
- 3.5.1、计算梯度
- 3.5.2、更新权重和偏置
- 4、小结
🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、什么是神经网络
人工神经网络( Artificial Neural Network, 简写为ANN)也简称为神经网络(NN),是一种模仿生物神经网络结构和功能的计算模型。
人脑可以看做是一个生物神经网络,由众多的神经元连接而成。
各个神经元传递复杂的电信号,树突接收到输入信号,然后对信号进行处理,通过轴突输出信号。
下图是生物神经元示意图: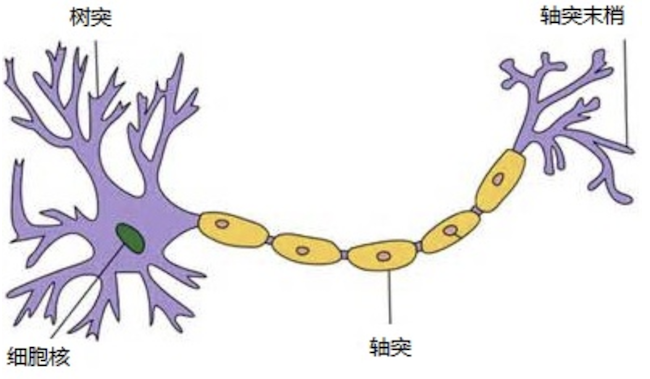
当电信号通过树突进入到细胞核时,会逐渐聚集电荷。达到一定的电位后,细胞就会被激活,通过轴突发出电信号。
2、人工神经网络
那怎么构建人工神经网络中的神经元呢?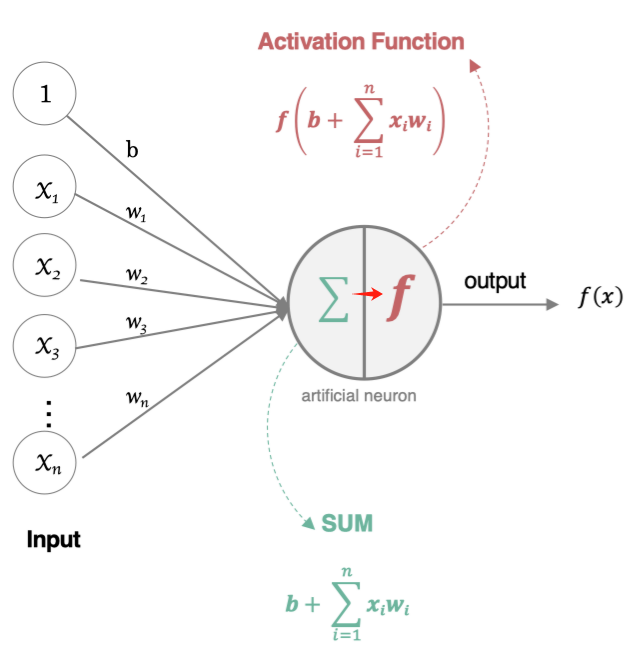
这个流程就像,来源不同树突(树突都会有不同的权重)的信息,进行的加权计算,输入到细胞中做加和,再通过激活函数输出细胞值。
接下来,我们使用多个神经元来构建神经网络,相邻层之间的神经元相互连接,并给每一个连接分配一个强度,如下图所示: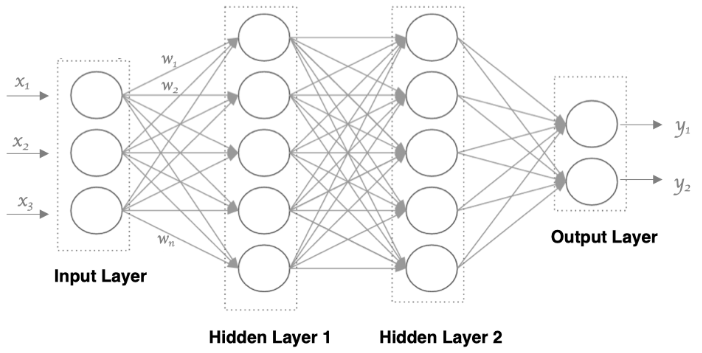
神经网络中信息只向一个方向移动,即从输入节点向前移动,通过隐藏节点,再向输出节点移动。
其中的基本部分是:
- 输入层:即输入 x 的那一层
- 输出层:即输出 y 的那一层
- 隐藏层:输入层和输出层之间都是隐藏层
特点是:
- 同一层的神经元之间没有连接
- 第 N 层的每个神经元和第 N-1层 的所有神经元相连(这就是full connected的含义)
- 第N-1层神经元的输出就是第N层神经元的输入
- 每个连接都有一个权值
3、多层感知器
详解上文提到的多层感知器: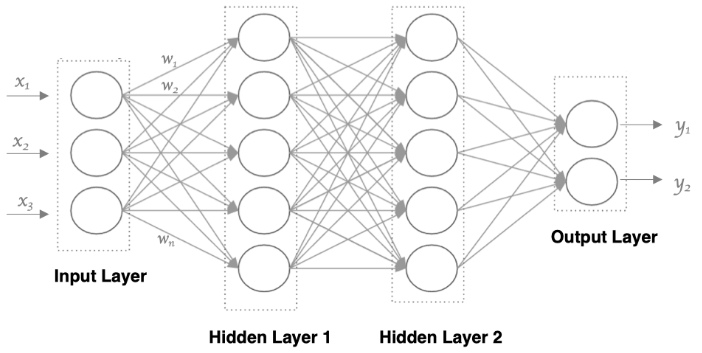
多层感知器 (Multilayer Perceptron, MLP) 结构
3.1、输入层
输入层: Input Layer
输入特征 (Input Features): ( x 1 , x 2 , x 3 ) ( x_1, x_2, x_3 ) (x1,x2,x3)
- 输入层的神经元数量等于输入特征的数量。
- 在这个例子中,有三个输入特征 ( x 1 , x 2 , x 3 ) ( x_1, x_2, x_3 ) (x1,x2,x3);输入特征可以来自数据集中的一个样本
3.2、隐藏层
隐藏层:Hidden Layers
3.2.1、隐藏层 1
- 这是网络中的第一个隐藏层,包含多个神经元。
- 每个神经元接收来自输入层的加权输入。
- 每个连接(线条)代表一个权重 ( w ) ( w ) (w),这些权重在训练过程中会被调整。
- 隐藏层神经元通过激活函数(例如 ReLU、Sigmoid 等)生成输出。
3.2.2、隐藏层 2
- 这是网络中的第二个隐藏层,包含多个神经元。
- 每个神经元接收来自隐藏层 1 的加权输入。
- 这些输入经过加权求和并通过激活函数生成输出。
3.3、输出层
输出层:Output Layer
输出 (Outputs): ( y 1 , y 2 ) ( y_1, y_2 ) (y1,y2)
- 输出层的神经元数量等于预测目标的数量。在这个例子中,有两个输出 ( y 1 , y 2 ) ( y_1, y_2 ) (y1,y2)。
- 每个输出神经元接收来自隐藏层 2 的加权输入。
- 输出神经元可以使用线性激活函数(对于回归任务)或其他激活函数(如 Softmax 对于分类任务)生成最终的预测值。
3.4、前向传播
前向传播:Forward Propagation
3.4.1、加权和⭐
加权和:Weighted Sum
- 每个神经元接收所有前一层神经元的输出,乘以各自的权重,并加上偏置项,然后计算加权和。
- 数学表达式: z j ( l ) = ∑ i = 1 n ( l − 1 ) w j i ( l ) a i ( l − 1 ) + b j ( l ) z_j^{(l)} = \sum_{i=1}^{n^{(l-1)}} w_{ji}^{(l)} a_i^{(l-1)} + b_j^{(l)} zj(l)=∑i=1n(l−1)wji(l)ai(l−1)+bj(l)
- 公式解释:
- ( l ) ( l ) (l) 表示当前层, ( j ) ( j ) (j)表示当前层的神经元索引,( i ) 表示前一层的神经元索引
- z j ( l ) z_j^{(l)} zj(l) 表示第 ( l l l) 层第 ( j j j) 个神经元的输入加权和。
- n ( l − 1 ) n^{(l-1)} n(l−1) 表示第 ( l − 1 l-1 l−1) 层的神经元数量。
- w j i ( l ) w_{ji}^{(l)} wji(l) 表示从第 ( l − 1 l-1 l−1) 层第 i i i 个神经元到第 l l l 层第 j j j 个神经元的权重。
- a i ( l − 1 ) a_i^{(l-1)} ai(l−1) 表示第 ( l − 1 l-1 l−1) 层第 i i i 个神经元的输出(激活值)。
- b j ( l ) b_j^{(l)} bj(l) 表示第 l l l 层第 j j j 个神经元的偏置。
3.4.2、激活函数
激活函数:Activation Function
- 加权和 ( z ) ( z ) (z)通过激活函数生成当前层神经元的输出。
- 数学表达式: a j ( l ) = f ( z j ( l ) ) a_j^{(l)} = f(z_j^{(l)}) aj(l)=f(zj(l))
- a j ( l ) a_j^{(l)} aj(l) 表示第 l l l 层第 j j j 个神经元的输出(激活值),其中 f f f 是激活函数。
3.5、反向传播
反向传播:Backward Propagation
3.5.1、计算梯度
计算梯度:Compute Gradients
- 反向传播从输出层开始,通过计算损失函数的梯度,逐层向前传播误差,计算每个权重和偏置的梯度。
- 数学表达式(举例说明): [ δ j ( l ) = ∂ L ∂ z j ( l ) ] [ \delta^{(l)}_j = \frac{\partial L}{\partial z^{(l)}_j} ] [δj(l)=∂zj(l)∂L]
- ( δ j ( l ) ) ( \delta^{(l)}_j ) (δj(l))是第 ( l ) ( l ) (l)层第 ( j ) ( j ) (j)个神经元的误差项, ( L ) ( L ) (L)是损失函数。
3.5.2、更新权重和偏置
权重和偏置:Weights and Biases
- 使用优化算法(如梯度下降)更新每个权重和偏置,以最小化损失函数。
- 数学表达式:KaTeX parse error: {align*} can be used only in display mode.
- 其中 ( η ) ( \eta ) (η)是学习率。
4、小结
什么是神经网络:神经网络就是模拟人神经元的工作机理,并构造仿生的神经元来解决实际问题
一个简单的神经网络,包括输入层、隐藏层、输出层,其中隐藏层可以有很多层,每一层也可以包含数量众多的的神经元
